| Theorie | Kabeltheorie | Diskussionsseite | Diskussion Kabel | Dämpfungs-Diskussion |
| ein wenig Kabeltheorie | Dr.-Ing. Gottlieb Strassacker
früher Dozent für Elektrotechnik an der Universität Karlsruhe |
|
Die meisten technisch interessierten Menschen wissen, dass ein sehr niederohmiger Ausgangswiderstand eines Endverstärkers die ungewollten Einschwingvorgänge von Lautsprechern bedämpfen soll und kann. Ist jedoch die Zuleitung vom Verstärker zu den Boxen nicht auch niederohmig, dann können die Lautsprecher nur ungenügend bedämpft werden. Daher neigen wir dazu, Zuleitungen mit möglichst großem Leitungsquerschnitt zu verwenden. Allerdings bedenken wir dann selten, dass im Audio-Frequenzbereich auch schon Stromverdrängung vorkommen kann. Für sehr niedere Frequenzen gilt ebenso wie für Gleichstrom das Ohmsche Gesetz mit einem Spannungsabfall U längs des Kabels. Dabei ist dieser Spannungsabfall mit R als Gleichstromwiderstand des Kabels und I als elektrischer Stromstärke darin: |
|
| (1) | U = I . R |
| Damit geht zusätzlich ein Teil der Leistung, z.B. eines Verstärkers, die den Boxen zugeführt werden soll, verloren. Diese Verlustleistung Pv in einem Kabel ist: | |
| (2) | Pv = I2 . R |
| wobei wieder I die Stromstärke im Kabel und R der Gleichstrom-Kabelwiderstand ist. (Damit diese Verlustleistungen auf 50 Hz-Überland-Hochspannungsleitungen nicht zu groß wird, erhöht man die Spannung auf einige hunderttausend Volt und kommt dadurch mit geringerer Stromstärke aus, um immer noch genügend Leistung von einem Kraftwerk z.B. in eine mittelgroße Stadt zu übertragen.) Entsprechend handeln auch HiFi-Freaks, da aber die Spannung von einem Highend-Verstärker zu den Boxen nicht erhöht werden kann, verwendet man oft größere Zuleitungsquerschnitte, mitunter sogar bis 16 mm2. | |
| Aber die großen Leitungsquerschnitte bei HiFi-Anlagen haben den Nachteil, dass im Bereich von 10 bis 20 kHz der Strom durch die schon erwähnte Stromverdrängung aus dem Leiterinneren nach außen hin verdrängt wird, wodurch die wirksamen stromführenden Kabelquerschnitte für die hohen Frequenzen kleiner sind als für die niederen Frequenzen. Dadurch ist der Leitungswiderstand für die hohen Frequenzen größer als für die niederen. Bei Gleichstrom gibt es keine derartige Stromverdrängung. Wir müssen also die Stromverdrängung näher betrachten. | |
Leitungsquerschnitt und Stromverdrängung |
|
| Da wir als Kabel in aller Regel kreisrunde Drähte verwenden, handelt es sich um allseitige Stromverdrängung. Auf die Herleitung der Formeln für diese allseitige Stromverdrängung, die über partielle Differentialgleichungen zu Besselfunktionen führt und recht kompliziert ist, soll hier verzichtet werden. Wir gehen gleich zu Näherungs-Endformeln über. Dabei gibt man das Verhältnis des elektrischen Widerstandes bei Stromverdrängung Rw zum Gleichstromwiderstand Rg an. Für geringe bis mittelstarke Stromverdrängung gilt solange X = ro(p f k m)1/2 /2 < 1 ist: | |
| (3) | Rw/Rg » 1+1+X4 /3 |
| Ist jedoch X = ro(p f k m)1/2 /2 > 1,dann gilt fogende Näherung: | |
| (4) | Rw/Rg » X+0,25 + 3 / 64X |
|
Die Gln.(3) und (4) sind recht einfach zu interpretieren. Die Stromverdrängung in einem kreisrunden Draht nimmt mit der Frequenz und dem Radius des Drahtes zu. Praktisch bedeutet dies, dass Stromverdrängung auch schon bei f = 50 Hz dann stattfinden kann, wenn der Radius eines Drahtes größer als 1cm wird. Nun verwenden wir zum Glück in der Audiotechnik keine so großen Drahtqueschnitte, dafür aber Frequenzen bis 20 kHz. Ist das Verhältnis Rw /Rg etwa gleich 1, dann wirkt sich praktisch keine Stromverdrängung aus. Ist es jedoch viel größer 1, dann liegt starke Stromverdrängung vor. Zugleich erhöht sich derjenige Teil der Induktivität des Kabels, der mit dem Magnetfeld innerhalb des Leiters zusammenhängt, nämlich dessen innere Induktivität Li, hier als Beispiel für X = ro(p f k m)1/2 /2 > 1: |
|
| (5) | wLi /Rg » X - 3/ 64X + 3/128X2 |
| Dabei bedeuten w die Kreisfrequenz 2pf, m die universelle magnetische Feldkonstante (absolute Permeabilität). Sie ist in Kupfer: m = 4p10-7 Vs/Am, k die Leitfähigkeit von Kupfer: k » 58 .106 A/Vm und ro ist der Radius des verwendeten Drahtes. Aber im Allgemeinen ist dieser Anteil der inneren Induktivität eines Stromkabels bei Niederfrequenz vernachlässigbar klein oder zumindest nur ein Bruchteil der Gesamtinduktivität. Bei Stegleitungen z.B. und Niederfrequenz ist die Gesamtinduktivität L = Li + La eines Kabels 5 bis 10 mal so groß wie dessen innere Induktivität Li. Insgesamt jedoch sorgen die innere Induktivität Li und die äußere Induktivität La zusammen mit dem Stromverdrängungs-Wirkwiderstand Rw für den Spannungsabfall im Kabel. Dabei kann dessen äußere Induktivität berechnet werden aus dem magnetischen Fluss durch den Steg zwischen den Rändern der beiden Drähte: | |
| (6) | La = Fa / I = m òò Ha da / I |
|
Dabei sind Fa der äußere magnetische Fluss, der sich als Flächenintegral über m mal der äußeren magnetischen Feldstärke Ha durch den Steg der Stegleitung ergibt. m ist wieder die universelle magnetische Feldkonstante und Ąda“ ist das von Ha durchsetzte Flächenelement. Wir wollen als Beispiel das Verhältnis Rw/Rg nach den Gln.(3) und (4) berechnen für die Kabelquerschnitte von 2,5, 4,0 und 16 mm2 . Ergebnis: |
|
| Drahtquerschnitt q = | 2,5 mm2 | 4 mm2 | 4 mm2 | 4 mm2 | 16 mm2 | 16 mm2 | 16 mm2 |
| Frequenz f = | 16 kHz | 2 kHz | 10 kHz | 16 kHz | 2 kHz | 10 kHz | 16 kHz |
| Rw / Rg | 1,18 | 1,00 | 1,17 | 1,37 | 1,08 | 2,00 | 2,43 |
| Rw pro m in Ohm | 0,00814 | 0,00431 | 0,00504 | 0,00590 | 0,00117 | 0,00216 | 0,00262 |
|
Man sieht, bei q = 2,5 mm2 hat man selbst bei 16 kHz mit Rw /Rg » 1,18 noch keinen bemerkenswert erhöhten Leitungswiderstand gegenüber Gleichstrom. Bei großen Drahtquer-schnitten jedoch (Beispiel hier: 16 mm2) ist der Widerstandsunterschied mit Rw /Rg » 2,43 zwischen niederfrequenten und hochfrequenten Strömen viel größer als bei kleineren Drahtquerschnitten (Beispiel hierzu: 4 mm2 ). Im Allgemeinen ist daher sehr wohl anzuraten, dass man sich mit einem Drahtquerschnitt von 4 mm2 begnügt und dadurch für niedere und hohe Frequenzen keine großen Widerstandsunterschiede in Kauf nehmen muss. |
|
|
Nur bei sehr starker Stromverdrängung besonders in der Hochfrequenztechnik werden die Formeln Gln.(3) und (4) noch einfacher. Man spricht dann vom Skin- oder Hauteffekt, weil Strom praktisch nur noch im äußeren Drahtrand oder in der Drahthaut fließt. Dann gilt als Näherungslösung: |
|
| (7) | Rw /Rg » wLi /Rg »ro/(2(wmk / 2)1/2 |
| (8) Abkürzung: | d = (2 / wmk )1/2 als äquivalente Leitschichtdicke gegenüber einer Gleichstrom führenden Drahtstärke |
 |
 |
|
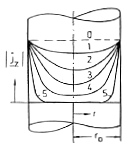
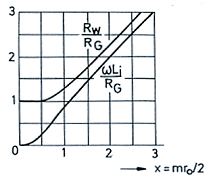
Links: Mit zunehmender Frequenz und zunehmendem Durchmesser zunehmende Stromverdrängung zur Außenhaut des Leiters hin, hier bezogen auf gleiche Drahtstärke. Rechts: Diagramm der Stromverdrängung: Rw /Rg und wLi /Rg. |
|
Leistungen und Energietransport in einem Kabel |
|
|
Auf die Frage, wo wird die elektrische
Energie eines Kabels transportiert, wird der Unvoreingenommene sofort
antworten: Natürlich im Draht des Kabels. Er wird umso mehr überrascht sein
zu erfahren, dass der Energietransport nicht im Drahtinnern, sondern im
Dielektrikum durch elektrisches und magnetisches Feld als Träger der Energie
erfolgt. Diese Behauptung müssen wir natürlich beweisen. Dazu benötigen wir
Vektoren, das sind hier nicht nur gerichtete Zahlenwerte wie in der
Mathematik, sondern physikalische Größen mit Zahlenwerten, Einheiten und
Richtung! Wir benötigen die Vektoren:
|
|
| (9) |
[ |
|
Schreibt man das Vektorprodukt
|
|
| (10) |
|
|
den Poyntingvektor der Energieströmung.
Tatsächlich jedoch ist seine Einheit, wie aus Gl.(9) folgt VA/m2,
also Flächendichte der Leistung. Dabei ist zu unterscheiden
zwischen einem Poyntingvektor
|
|
|
Richtungszuordnung:
Die Vektoren
|
|
|
Einsvektoren: |
|
 |
|
|
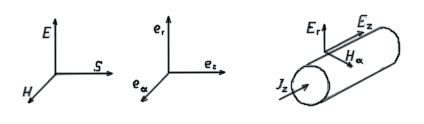
An und in einem kreiszylindrischen Draht verwendet
man sinnvollerweise die vorangehend auch gezeichneten Zylinderkoordinaten
mit den ebenso rechtswendig in folgender Reihenfolge einander zugeordneten
Einsvektoren:
|
|
|
Wir betrachten jetzt zuerst die Felder
innerhalb eines Drahtes. Infolge des Drahtwiderstandes erzeugt der Strom in
Achsrichtung den oben schon genannten Spannungsabfall. Dieser bezogen auf
die Längeneinheit ist die Komponente der elektrischen Feldstärke Ez im
Leiter. Die magnetische Feldstärke ist rechtswendig zur Leitungsstromdichte
zugeordnet, das magnetische bildet also sowohl innerhalb wie auch außerhalb
eines einzigen kreisrunden Drahtes Kreise. Wir haben daher im Draht die
Komponente Ha. Wegen des Rechtssystems
von |
|
| (11) | Sr = Ez Ha(r) = Ez Jz p r2/ 2pr = Ez r Jz / 2 |
|
Jz ist die Leitungsstromdichte Jz = I / p r2, die wir hier als konstant über den Drahtquerschnitt voraussetzen. Sr ist daher eine reine Verlustleistungsdichte. Wird sie über die Gesamtoberfläche der Drähte integriert, so erhält man die Verlustleistung im Draht Pv = I2 . R. Andere Leistungen, insbesondere diejenige, die zum Verbraucher (den Boxen) transportiert wird, kommt im Drahtinnern nicht vor! Wir untersuchen daher nun das Dielektrikum um die Drähte herum. |
|
|
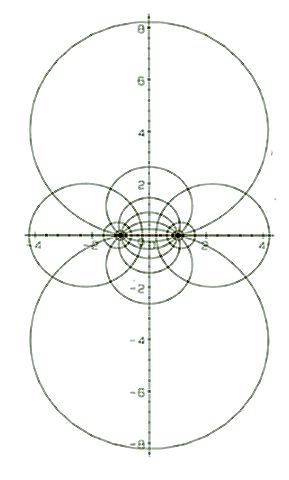
Vektoren stehen tangential an den gezeichneten Feldlinien des Feldverlaufs der Paralleldrahtleitung
An den Drahtoberflächen hat der Vektor
Dadurch lautet das Vektorprodukt |
|
| (12) |
|
|
Dies war zu zeigen. Die ganze zum Verbraucher transportierte Energie wird im Dielektrikum und nicht im Drahtinnern transportiert. Und bei genauerer Betrachtung durch Hinzunahme von Ez wird deutlich, dass der Energie transportierende Vektor nach Gl.(11) ein wenig schräg zur Drahtachse steht, da auch die Verlustleisung innerhalb der Drähte aus der im Dielektrikum vorhandenen und im Dielektrikum transportierten Energie entnommen wird. |
|
 |
Literaturhinweise:
Küpfmüller / Kohn, THeoretische Elektrotechnik und Elektronik, eine Einführung, Springer, 15. Auflage 1999 Gottlieb Strassacker, Rotation, Divergenz und das Drumherum, eine Einführung in die Elektromagentische Feldtheorie, Teubner, 4. Auflage 1999. Strasssacker / Strassacker, Analytische und numerische Methoden der Feldtheorie, Teubner 1993. |