| Lautsprecherbau | Grundlagen | Verstärkergrundlagen |
 Dr.-Ing. Gottlieb Strassacker
Dr.-Ing. Gottlieb Strassacker
Dozent an der Universität Karlsruhe in Ruhestand |
Ohmsches Gesetz, Leistung und Energie
Eine Einführung für Unkundige
1. Gleichstrom
1.1 Ohmsches Gesetz
Wir beschäftigen uns mit elektrischer Spannung, elektrischem Strom und elektrischen Widerständen. Nachfolgend lassen wir das ''elektrisch'' weg und sprechen nur von Spannung, Strom und Widerstand. Da wir zuerst von Gleichstrom reden, denken wir an Batterien jeder Art, an Akkus und an gleichgerichtete Wechselspannungen als Spannungsquellen.
Um das Verständnis anzuregen sei gesagt: So wie der Druck in der städtischen Wasserleitung das Wasser durch einen Wasserschlauch drückt, so drückt die Spannung den Strom durch einen (elektrischen) Widerstand. Dabei werden bezeichnet:
Spannung durch U oder u(t) oder nur u; sie wird gemessen in Volt, Kurzzeichen V.
Strom durch I oder i(t) oder nur i; sie wird gemessen in Ampere, Kurzzeichen A
Widerstand R, gemessen in Ohm, Kurzzeichen Ω.
Wie oben angedeutet, treibt die Spannung U den Strom I durch einen Widerstand R. Es leuchtet ein, dass der Strom umso größer wird, je größer die antreibende Spannung oder je kleiner der (behindernde) Widerstand ist. Braucht man aber einen bestimmten Strom durch einen vorgegebenen Widerstand, z.B. einen Lautsprecher, dann muss die Spannung entsprechend groß sein. Diesen Zusammenhang beschreibt das Ohmsche Gesetz: U=I · R.
Früher, als Soldaten in Fernmeldeeinheiten arbeiten sollten, aber der Elektrotechnik noch nicht mächtig waren, sagte man ihnen, "denkt einfach an Unser Infanterie Regiment", dann erinnert ihr euch, dass U=I · R ist. Da wir heute aber nicht mehr militaristisch, dafür aber öfter im Urlaub sind, auch in der schönen Schweiz, sagen wir lieber "denkt an den Kanton U-R-I. Also U = R · I. Denn es ist gleichgültig, ob man zuerst R oder zuerst das I schreibt, es ist das Produkt R· I = I · R.
Aber nicht immer will man die Spannung U berechnen. Mitunter interessiert auch der Widerstand R oder der Strom I aus den beiden anderen gegebenen Größen. Bringt man einen multiplikativ genommenen Wert auf die andere Seite des Gleichheitszeichens, so kommt er dort in den Nenner. man kann auch sagen, man teilt beide Seiten einer Gleichung durch I (oder durch R) und erhält als Ergebnis U/I=R (oder U/R=I). In Worten: Strom ist Spannung U geteilt durch Widerstand R oder Widerstand R ist Spannung U geteilt durch Strom I.
Man kann diese Formel auch als Dreieck anschreiben und erhält die jeweils gesuchte Größe, indem man sie mit dem Finger abdeckt:
U
(1)
I · R
Deckt man das gesuchte I ab, so erhält man es aus U/R und R abgedeckt erhält man aus U/I.
Ein Rechenbeispiel: Ein Autofahrer will im Winter in einem längerem Stau einen Heizzofen an seine Autobatterie (korrekter: Autoakku) anklemmen, um nicht zu sehr zu frieren. Der Widerstand des Heizofens sei 50 Ohm. Welcher Strom fließt durch den Heizofenwiderstand? Lösung: I = U / R = 12 V / 50 Ω = 0,24 A. Nachher werden wir sehen, welche Leistung dies ist.
1.2 Leistung und Energie bei Gleichstrom
Elektrische Leistung gibt Auskunft darüber, wieviel Energie pro Zeiteinheit verbraucht wird. Umgekehrt ist Energie das Produkt aus Leistung mal Zeit. Energie ist das, was ein Verbraucher den jeweiligen Stadtwerken bezahlen muss. Ist die momentane Leistung gering (groß), dann ist auch das zu bezahlende Produkt aus Leistung mal Zeit gering (groß). Leistung und Energie werden gemessen und bezeichnet als:Leistung durch P, gemessen in Watt oder Kilowatt, Kurzzeichen W oder kW (k = 1000),
Energie durch E, gemessen in Wattstunden oder Kilowattstunden, Kurzzeichen Wh oder kWh
(h steht für Stunden).
Formelmäßig ist bei Gleichstrom
(2)
Leistung = Spannung · Strom = U · I
Energie = Leistung P · Zeit t = Spannung · Strom · Zeit = U · I · t = P · t
Zurück zu unserem obigen Beispiel. Der Autofahrer, der einen 50 Ohm Heizofen an den 12 Volt Autoakku anschließt, erzeugt damit eine Leistung von 12 V · 0,24 A = 2,88 Watt. Er wird also nicht viel Freude mit dieser geringen Heizwirkung haben. Denn normalerweise hat ein Heizofen, der an das Stadtnetz von 230 V angeschlossen wird, die etwaige Leistung von U·I=U·U/R = 230 V· 230 V / 50 Ω = 230 V · 4,6 A = 1058 Watt.
Die Energie des Autoakkus würde auch nur wenig in Anspruch genommen. Sie wäre ja 12 V · 0,24 A · 2 h = 12,76 Wh, wenn der Heizofen zwei Stunden angeschlossen gewesen wäre. Insgesamt hat eine Autoakku eine Energie gespeichert von etwa 530 bis 1320 Wh, beim Kauf meist beschrieben durch die Ampere-Stundenzahl von etwa 44 bis 110 Ah bei der Nennspannung von 12 V.
2. Wechselstrom
2.1 Ohmsches Gesetz für Wechselstrom
Schaltet man einen Kondensator in einen Gleichstromkreis, z.B. in den einer Batterie, so unterbricht der Kondensator den Strom, es fließt kein Strom, da ein Kondensator für Gleichstrom ein unendlich
großer Widerstand ist. Anders bei Wechselspannung und -Strom.
Schaltet man eine Spule in einen Gleichstromkreis, so verringert nur deren Gleichstromwiderstand die Stromstärke, nicht aber ihr induktiver Widerstand. Anders bei Wechselspannung und -Strom. Wir müssen daher das ohmsche Gesetz für Wechselspannung und -Strom gesondert behandeln.
Einige Begriffe sind zu erweitern. So gibt es bei Wechselspannung nicht nur einen ohmschen, sondern auch einen induktiven Widerstand von Spulen XL und einen kapazitiven Widerstand von Kondensatoren XC. Und während wir bei Gleichspannung nur einen Spannungswert hatten, gibt es bei Wechselspannung den Spitzenwert û, der Amplitude heißt, einen Effektivwert, der hier mit U bezeichnet wird, da er so definiert ist, dass er die gleiche Stromwärmeleistung hervorbringt wie eine ebenso große Gleichspannung.
Hier der zeitliche Verlauf einer sinusförmigen Spannung mit der Amplitude (Ampl) und dem Effektivwert Uef:
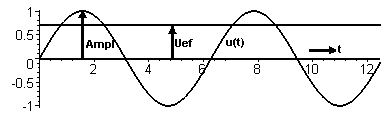
Entsprechendes gilt auch für Strom. Es gibt für ihn auch einen Spitzenwert, die Amplitude î und den Effektivwert, den wir auch als I bezeichnen wie bei Gleichstrom, da er an einem ohmschen Widerstand auch die gleiche Stromwärme erzeugt wie ein ebenso großer Gleichstrom:
Wir wenden uns jetzt dem ohmschen Gesetz für Wechselstrom zu. Es lautet für die Scheinwiderstände Z, die Scheinleitwerte Y = 1 / Z und die Effektivwerte von Spannung und Strom:
(3) Effektivwert = Amplitude / Wurzel aus 2 = 0,707 · Amplitude
(3a) U = Uef = 0,0707 · û ; I = Ief = 0,0707 · î
Misst man mit Effektiv-Spannungs- und Strommessern die Spannung und den Strom an ein oder zwei zusammen geschalteten Widerständen, so ist der Scheinwiderstand Z der Quotient aus gemessener Spannung und gemessenem Strom. Dabei können sich, wie wir sehen werden, Widerstände komplizierter als nur durch eine Summe zusammensetzen. Das gleiche gilt für Scheinleitwerte Y. Der Scheinwiderstand Z ist also scheinbar die Widerstandssumme z.B. aus einem Wechselstrom-Spulenwiderastand und einem ohmschem Widerstand, tatsächlich jedoch ist Z der Strom begrenzende Wert aus beiden; Entsprechendes gilt für den Scheinleitwert Y:
(4) U = I · Z; I = U / Z; oder I = U · Y
Nun etwas Überraschendes. Wir schalten eine fast verlustlose Spule (ohne merklichen ohmschen Verlustwiderstand) und einen ohmschen Widerstand R in Serie. Wir legen diese Serienschaltung an die 5 V Wechselspannung eines Klingeltrafos und messen die Effektivwerte der drei Spannungen. Dabei kann z.B. als Messergebnis herauskommen: Spannung am ohmschen Widerstand = 4 V, Spannung an der verlustlosen Spule = 3 V. Addieren wir beide, so sollte doch die Gesamtspannung des Klingeltrafos, unsere 5 V, herauskommen, aber die Summe ist 7 V. Wir zweifeln an der Spannung des Klingeltrafos und messen nochmals nach. Ja, es sind nur 5 V. Aber 4 V + 3 V = 7 V ! Wo liegt die Ursache? Das folgende Bild gibt Auskunft.
Der Scheinwiderstand Z ist zwar, wie das ohmsche Gesetz aussagt, der Quotient aus Spannung und Strom. Aber sind wie hier ein ohmscher Widerstand R und ein induktiver Widerstand X = ωL in Serie geschaltet, dann ist deren Scheinwiderstand Z = (R2 + X2)1/2. Dieses etwas komplizierte Verhalten wird durch folgendes Bild deutlich.
Links: Schaltbild, Mitte: Widerstandsdreieck, rechts: Spannungsdreieck:
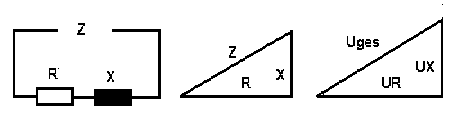
Der induktive Wechselstromwiderstand X = ωL einer verlustlosen Spule ist in der graphischen Darstellung senkrecht zum ohmschen Widerstand R anzuordnen. Daher ist Z nicht R + X, sondern die Wurzel aus der Summe der Quadrate beider Widerstände. Die Folge davon ist, dass auch die zugehörigen Spannungen von Spule und ohmschem Widerstand senkrecht zueinander anzuordnen sind. Dabei gilt für die Spannungen ein zu den Widerständen proportionales Dreieck mit der Trafospannung Uges sowie UX an der Spule und UR am Widerstand R.
Man muss also rechtwinklige Dreiecke zeichnen mit ohmschem Widerstand R und induktivem Spulenwiderstand X als Katheten, dann ist die Hypothenuse (nach dem Satz des Pythagoras für rechtwinklige Dreiecke) die Gesamtspannung: (32+42)1/2 V = 5 V.
Will man umgekehrt die Spannung an der Spule berechnen und zwar aus der gegebenen Trafospannung von 5 V und 4 V am ohmschen Widerstand dann ist zu rechnen: (52 - 42)1/2 V = 3 V.
L ist die Induktivität einer Spule mit der Einheit Henry (H) = Vs/A meist mH =10-3H
C ist die Kapazität eines Kondensators mit der Einheit Farad (F) = As/V meist
µF = 10-6F
Der induktive Widerstand einer Spule, also ihr Blindwiderstandsanteil, der senkrecht zum ohmschen oder Verlustwiderstand aufgetragen wird, ist:
(5) XL = ωL = 2πf · L
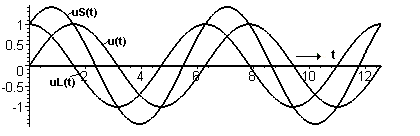
Dass die Widerstände R und XL rechtwinklig zueinander stehen, wird verständlicher, wenn man erkennt, dass auch Augenblickswerte der Wechselspannungen gegen einander zeitlich verschoben sind. Das folgende Bild zeigt die sinusförmigen Spannungen an einer Serienschaltung von Spule und Widerstand mit der Eingangsspannung uS(t), der Spannung am ohmschen Widerstand u(t) und der gegen u(t) um 90o voraus eilenden Spannung uL(t) an einer verlustlosen Spule. Man sieht, die Summenspannung uS(t) ist nur das Wurzelzweifache der Einzelspamnnungen und nicht deren doppelter Wert:
Andererseits ist der kapazitive Widerstand XC eines Kondensators, also sein Blindwiderstand, auch senkrecht zum ohmschen Verlustwiderstand aufzutragen, aber wie wir schon wissen, entgegengesetzt zum induktiven Blindwiderstand XL:
(6) XC = - 1 / (ωC) = - 1 / (2πf ·C)
Daher gilt für die Zusammenschaltung von ohmschem Widerstand und Kondensator die Grafik des folgenden Bildes. Der Kondensator hat, wie wir sehen, bei Wechselspannung einen von der Frequenz ω = 2 π f abhängigen Widerstand und nicht einen unendlich großen Widerstand wie bei Gleichstrom. Schaltet man beide, induktiven und kapazitiven Widerstand in Serie, so ist die Widerstandssumme von Kondensator und Spule: Z = XL + XC = ωL - 1/(ωC) , also die erwähnte Differenz!
Im folgenden Bild schalten wir zur Spule mit der Induktivität L und Kondensator mit der Kapazität C noch einen ohmschen Widerstand in Serie. Dadurch wird das Verhalten dieser drei Bauelemente bezüglich ihrer Widerstandssumme, im Pfeildiagramm rechts, noch deutlicher.
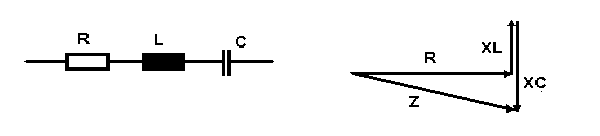
Dass der kapazitive Widerstand XC vom induktiven Wechselstromwiderstand XLabgezogen wird, hängt von der zeitlich um π/2 unterschiedlichen Energiespeicherung von Spule und Kondensator ab. In Phasen hohen Stromes ist die induktive Energie groß aber die kapazitive klein; umgekehrt ist in Phasen geringen Stromes die kapazitive Energie groß aber die induktive Energie klein.
Für den Scheinwiderstand dieser Serienschaltung von drei Bauelementen R, L und C gilt die Formel:
(7) Z = [ R2 + (ωL -1/ωC)2]1/2
Damit kann das ohmsche Gesetz auf diese Serienschaltung angewandt werden. Die Spannung ist proportional zu Z, der Proportionalitätsfaktor ist der Strom I:
(8) U = I · [ R2 + (ωL -1/ωC)2]1/2
Wir könnten jetzt eine Theorie der Schwingungskreise beginnen, denn obige Schaltung ist ein Serienschwingkreis, aber das ist nicht Gegenstand dieser Einführung. Es ist dagegen erforderlich, noch einige Worte zu Parallelschaltungen zu verlieren. Dabei addieren sich wieder die Leitwerte, wie das auch bei Gleichstrom der Fall war. Diese sind:
Leitwert eines ohmschen Widerstandes: G = 1 / R;
Induktiver Leitwert einer idealen, verlustlosen Spule: GL = 1 / XL = - 1 / (ωL)
Induktiver Leitwert einer mit R verlustbehafteten realen Spule: Siehe komplexe Rechnung.
Kapazitiver Leitwert eines idealen, verlustlosen Kondensators: GC = 1 / Xsub>C
= 1 / (ωC)
Der kapazitive Leitwert eines verlustbehafteten Kondensators ist ebenfalls der Anleitung zum ohmschen Gesetz mit komplexer Rechnung zu entnehmen. Zum Glück jedoch sind viele Kondensatoren sehr verlustarm, sodass ihr Verlustwiderstand oft ohne großen Fehler vernachlässigt werden darf.
Dass das Minuszeichen jetzt vertauscht beim Spulenleitwert - 1 / (ωL) auftaucht, ist kein Fehler, sondern ein Ergebnis der Theorie (siehe ohmsches Gesetz und komplexe Rechnung).
Werden nun analog zu unserem obigen Beispiel ein ohmscher Widerstand , eine verlustlose Spule und ein verlustloser Kondensator zueinander parallel geschaltet, dann begeht man durch die angenommene Verlustlosigkeit von Spule und Kondensator keinen wesentlichen Fehler, denn deren Verluste können in den Parallelwiderstand mit einbezogen sein. Der Summenleitwert der Parallelschaltung (des Parallelschwingkreises) ist :
(9) Y = [ G2 + ( GL -GC)2 ]1/2 Dazu links das Schaltbild, rechts das Leitwertdiagramm:
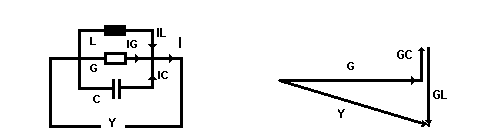
2.2 Leistung und Energie bei Wechselstrom
Leistung P wird, wie wir schon wissen, gemessen in W oder kW. Man hat zu unterscheiden zwischen Wirk-, Blind- und und Scheinleistung. Scheinleistung ist das Produkt aus den Effektivwerten von Strom und Spannung und zu berechnen nach:(10) P = Uef Ief
Sie beinhaltet Wirk- und Blindleistung (siehe unten). Durch die Stromstärke Ief werden auch die Leitungen belastet und erwärmen sich. Diese Leitungswärme ist Wirkleistung an ohmschen Widerständen. Wirkleistung ist die Leistung, die man bezahlen muss und die an Verlustwiderständen auftritt; sie ist definiert zu:
(11) Pw = Uef Ief cos(φ)
Dabei ist φ derjenige Phasenwinkel oder Phasenunterschied, der zwischen den Momentanwerten von Strom i(t) und Spannung u(t), also bei deren Schwingungen, als Differenzwinkel vorkommt. An Stromwärme erzeugenden Widerständen ist φ = 0 Grad und daher cos(φ) =1, so dass
Pw = Uef Ief ist.
An Blindwiderstäden XL und XC ist φ = 90 Grad und daher ist cos(φ) = 0, so dass Pw = 0 wird. Daher heißt diese Leistung Blindleistung Pb . Sie ist für sinusförmige Spannung und Stromstärken definiert zu:
(12) Pb = Uef Ief sin(φ)
Da wir jetzt Wirk-, Blind- und Scheinleistung kennen, können wir diese zusammenfassen. Es gilt:
(13) Pw2 + Pb2 = Ps2
Den Stadtwerken muss man, was schon angedeutet wurde, nur die in den Energiezählern (landläufig: "Stromzählern") gemessene und angezeigte, verbrauchte Energie E bezahlen. Sie ist das Produkt aus Wirkleistung Pw und der Zeit t, während der die Wirkleistung entnommen wird. Das ist
(14) E = Uef Ief cos(φ) t
Da wir aber nicht immer die gleiche, sondern unterschiedliche Wirkleistungen unserem Stadtnetz entnehmen, ist die Berechnungsformel diesem Wechsel anzupassen. Das macht der Energiezähler automatisch. Rechnerisch benutzen wir zum Summieren dieser Teilprodukte der Wirkleistung zur Gesamtsumme ein Integral und dessen zeitlichen Mittelwert; denn Wirkleistung ist allgemein definiert als zeitlicher Mittelwert der Leitungsschwingung u(t)i(t) in den zeitlichen Grenzen des Verbrauches von zum Beispiel von 0 bis t1:
(15) (1/tt1) ∫0t1 u(t) i(t) dt
Hier will ich mit der reellen Darstellung des ohmschen Gesetzes enden. Denn die aufwendigeren Schaltungen lassen sich leichter mit komplexer Rechnung bearbeiten. Diese findet der verehrte Leser im Artikel "Ohmgesetz komplex und einfache Filter".
zurück zur Übersicht