Dr.-Ing. Gottlieb Strassacker Dozent an der Universität Karlsruhe in Ruhestand

Ohmgesetz komplex und einfache Filter

1. Allgemeine Grundlagen

Ein in x- und in y-Richtung aufgetragenes Wertepaar eines ebenen Graphen kann in einer so genannten komplexen Ebene dargestellt werden. Allgemein gilt für das Wertepaar a und b: z = a + jb. Dabei gibt der Faktor j an, dass der damit multiplizierte Zahlenwert b ein y-Wert ist, also in y-Richtung in die komplexe Ebene eingetragen werden muss, während die Zahl a der x-Wert ist. Zur Kennzeichnung unterstreichen wir die komplexen Größen, die rechts vom Gleichheitszeichen einen Real- plus j ·Imaginärteil haben, um ihre Komplexität deutlich zu machen. Beispiele: z für Zahlen, Z für Widerstände, Y für Leitwerte, u und U für Spannungen.

Beispiel für Widerstände: Z = R+jX. Dabei ist Z ein komplexer Widerstand, der aus dem ohmschen Anteil R als Realteil und dem Blindwiderstand X als Imaginärteil besteht. Genauer: X ist der induktive Blindwiderstand X = ωL einer verlustbehafteten Spule oder der ganze Blindwidwiderstand einer als verlustlos angenommenen Spule. Beinhaltet X ein negatives Vorzeichen, dann handelt es sich um einen (verlustbehafteten) Kondensator mit dem kapazitiven Blinderstand X = -1/(ωC). Somit lautet der verlustbehaftete komplexe Kondensatorwiderstand: Z = R+1/(jωC). Erweitert man aber dieses 1/(jωC) mit j, so wird in dessen Nenner j² = -1, und der Zähler erhält ein j; denn j ist definiert durch j = (-1)^1/2.

(1)          j/j · (1 / jωC) = j / (j²ωC) = +j / (-ωC) = - j / (ωC). .

Einfaches Beispiel: Addition von zwei in Serie geschalteten Widerständen. Wir verstehen unter einem komplexen Widerstand, wie gerade beschrieben wurde, einen Widerstand, der sowohl einen ohmschen (=Verlust- oder Stromwärmeanteil) R als auch einen Induktivitätsanteil X_L = ωL und/oder einen Kapazitätsanteil X_C = -1/ωC enthält. Dann gilt für die Zusammenschaltung von R₁ und X_L mit R₂ und X_C als Serienschaltung:

(2)           Z₁ = R₁ + j X₁   und   Z₂ = R₂ +j X₂

und deren Summe ist:

(3)           Z_ges = (R₁ + R₂) + j (X₁ + X₂)

Damit lautet das ohmsche Gesetz in komplexer Schreibweise, wenn wir U für den komplexen Effektivwert der Spannung und I für den komplexen Effektivwert des Stromes verwenden:

(4)             U = Z I     oder     I = U Y

Werden dagegen zwei Widerstände parallel geschaltet, so sind deren komplexe Leitwerte Y zu addieren. Diese muss man sich in der Regel aus den komplexen Widerständen Z durch Invertieren verschaffen. Einen komplexen Leitwert erhält man aus dessen komplexem Widerstand wie folgt:

(5)           Y = 1 / Z = 1 / (R+jX) = (R-jX) / (R² + X²)

Wir haben dabei den Bruch erweitert, d.h. Zähler und Nenner wurden mit R-jX multipliziert. Dadurch wurde der Nenner reell d.h. frei von der imaginären Einheit j. Um die Summe zweier Leitwerte zu erhalten, müssen wir nun den Index 1 für den komplexen Widerstand 1 bzw. den Index 2 für den komplexen Widerstand 2 einsetzen und reelle Größen zu einander und imaginäre Größen zu einander addieren. Dann wird deren Summe aus den obigen Ergebnissen:

(6)          Y_ges = Y₁ + Y₂ = (R₁ - j X₁) / (R₁² + X₁²) +(R₂ -j X₂) / (R₂² + X₂²).

Die zwei Brüche können nicht ohne Weiteres zu einem einzigen Bruch zusammengefasst werden, da ihre Nenner im Allgemeinen verschieden sind. Das kann man an einem Zahlenbeispiel sehen und beheben. Wir nehmen an, es seien:

(7)          Z₁ = 3+j4 Ω    und    Z₂ = 6+j8 Ω

Durch Parallelschalten dieser beiden komplexen Widerstände nach der vorangehenden Formel (6) bekommen wir mit S = Siemens als gängige Einheit für 1/Ohm:

(8)          Y_ges = (3-j4) / (9+16) S + (6-j8)/(36+64) S = (3-j4) / 25 S + (6-j8) / 100 S.

Der erste Bruch ist mit dem Faktor 2, der zweite mit 1/2 zu erweitern, dann können die Brüche mit gleichen Nennern zu einem resultierenden komplexen Leitwert addiert werden:

(8a)          Y_ges = {(6-j8) / 50 + (3-j4) / 50} S = (9-j12) / 50 S = (0,18 - j0,24) S.

Man erkennt schon an diesem einfachen Beispiel, dass die Berechnung mehrerer, teils seriell, teils parallel geschalteter Widerstände rein rechentechnisch etwas aufwendig werden kann.

Gelegentlich benötigt man den Moivreschen Satz. Er erklärt näher, was mit j mathematisch noch gemacht werden kann. Er wird dann verwendet, wenn man Momentanwerte von Strom und Spannung nach Betrag und Phasenwinkel berechnen will. Er lautet:

(9)          e^jπ/2 = cos(π/2) + j sin(π/2) = cos(90^o) + j sin(90^o ) = 0 + j ·1 = j.

Wir haben bisher stillschweigend akzeptiert, dass j die y-Richtung vorschreibt. Tatsächlich aber ist j mehr. Wir wenden den Moivreschen Satz an und zwar jetzt mit ωt als variablem Argument:

(10)          e^jωt = cos(ωt) + j sin(ωt)

In der gerade angegebenen Form des Moivreschen Satzes wird mit der Zeitvariablen t, mit der Kreisfrequenz ω=2πf, wobei π=3,14159 ist und mit der Frequenz f in Hz gerechnet.

Genauer betrachtet, ist e^jωt ein Punkt auf einem Einheitskreis (Radius = 1 Längeneinheit), der mit zunehmendem Argument ωt im Gegenuhrzeigersinn, d.h. mathematisch positiv rotiert. Bei j = e^jπ/2 schneidet der rotierende Punkt die, wie wir aus Gleichung (9) sehen, imaginäre Achse mit den Werten j = 1 und x = 0.

Multipliziert man den Moivreschen Satz beidseitig z.B. mit einer Spannungsamplitude û, dann wird

(11)          û e^jωt = û cos(ωt) + j û sin(ωt)

In Gl.(11) steht links des Gleichheitszeichens ein Ausdruck, der die ganze komplexe Ebene durch Polarkoordinaten abdeckt, denn û ist der vom Nullpunkt aus gemessene Betrag und e^jωt kann jeden Winkel annehmen. Polarkoordinaten beinhalten also den Drehzeiger e^jωt, multipliziert mit einer Länge z.B. wie hier mit û und sind demnach für t = const ein ruhender, für laufendes t ein rotierender Zeiger. Rechts des Gleichheitszeichens von Gl.(11) stehen eine x- und eine y-Komponente, die die komplexe Ebene als kartesische Koordinaten mit Real- und Imaginärteil abdecken.

2. Anwendungen

2.1 Komplexe Spannungsteiler

Für uns ist es besonders interessant, hier einfache Filter aus Widerständen, Spulen und Kondensatoren zu berechnen. Wir nutzen dazu die Kenntnis des Spannungsteilers aus. Wir wollen langsam und verständlich Stück für Stück erarbeiten. Als einfachstes der einfachen Beispiele verwenden wir einen von der Frequenz unabhängigen Spannungsteiler, der aus zwei ohmschen Widerständen besteht. Wir nehmen bei der Berechnung an, dass die Folgeschaltung hochohmig ist, so dass der Ausgangsstrom I₂ = 0 wird, zumindest in guter Näherung. Hierbei können Effektivwerte bei sinusförmiger Wechselspannung verwendet werden. (Ein Effektivwert ist bei sinusförmigen Vorgängen gleich dessen Amplitude oder Höchstwert dividiert durch die Wurzel aus 2, also durch 1,414. Dann wird der Effektivwert des Stromes I = 0,707 î, der der Spannung U = 0,707 û ).
Schaltbild:

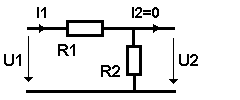
(12)        U₂ / U₁ = I₁R₂ / (I₁R₁ + I₁R₂) = R₂ / (R₁ + R₂)

Jetzt berechnen wir mit komplexen Amplituden
(= Amplituden harmonischer Größen, die komplex sein können,) den einfachsten Tiefpass, bestehend aus Wirkwiderstand R und Kondensator mit der Kapazit"at C. Wir verwenden wieder das Prinzip des Spannungsteilers unter der Voraussetzung, dass I₂ = 0 ist. Wir schreiben die Spannungen als komplexe Amplituden, û für Spannung und î für Strom, an mit 1/jωC = j(-1/ωC) = jX_C.
Schaltbild:

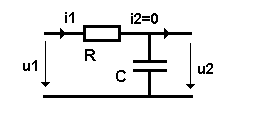
(13)        

û₂ / û₁ = j X_C / (R + j X_C) = 1 / jωC / (R + 1 / jωC)

Erweitern wir Gl.(13) mit jωC, dann wird einfacher:

(13a)          û₂ / û₁ = 1 / ( jωRC + 1)

Davon interessiert vor allem der Betrag, den man auch gerne als Graph aufzeichnet. Er ist die Wurzel aus Realteil im Quadrat plus Imaginärteil im Quadrat. In Gl.(13a) ist der Realteil gleich 1, der mit j multiplizierte Imaginärteil ist ωCR, so dass:

(14)          |û₂ / û₁| = U₂ / U₁ = 1 / [1+ (ωCR)²]^1/2

Die folgende Steigerung ist ein Tiefpass, der im Längszweig der Schaltung eine Spule, im Querzweig einen Kondensator enthält. beide Bauelemente sind nahezu verlustfrei, so dass wir keine ohmschen Widerstände berücksichtigen müssen. Der Betrag des komplexen Spannungsteilers lautet:

(15)          |û₂ / û₁| = U₂ / U₁ = | [ 1 / (jωC) ] / [ 1 / (jωC) + jω L ] | = 1 / (1 - ω²LC)   

Schaltbild:

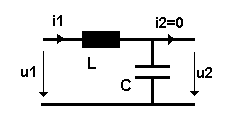
Da wir nur Blindwiderstände jωL und 1/jωC verwendet haben, hebt sich, wie Gl.(15) zeigt, die imaginäre Einheit j heraus und wir erhielten ein reelles Ergebnis. Man kann das Ergebnis noch vereinfachen, wenn man die Grenzfrequenz dieses Tiefpasses wie üblich definiert zu ω_g² = 1/LC:

(16)          ω_g² = 1/LC,     womit     U₂ / U₁ = 1 / (1 - ω² / ω_g² )

Da die Kreisfrequenz ω=2πf ist und die Grenzkreisfrequenz ω_g=2πf_g, ist das Verhältnis ω² / ω_g² = (f / f_g)². Aus Gl.(16) wird damit

(17)          U₂ / U₁ = 1 / (1- (f / f_g)²)

Dies ist eine Normierung, die noch deutlicher wird, wenn wir (f / f_g) durch die Verhältniszahl v ersetzen, so dass

(17a)          U₂ / U₁ = 1 / (1- v²)

wird. Sie hat den Vorteil, dass für unterschiedliche Grenzfrequenzen f_g beim Zeichnen nur eine Grafik gebraucht wird, während in der Formel nach Gl.(15) für jede Grenzfrequenz d.h. für jedes Produkt LC eine neue Grafik erforderlich ist.

Wir können analog zu dem gerade beschriebenen Tiefpass den entsprechenden Hochpass berechnen. Dazu müssen in der Schaltung lediglich Spule und Kondensator miteinander vertauscht werden. Für den wieder angewandten Spannungsteiler gilt:

(18)          û₂ / û₁ = jωL / (jωL + 1/jωC) = - ω²LC / (1 - ω²LC)     Schaltbild:

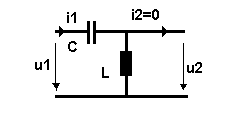
Das Ergebnis ist wieder reell wegen der angenommenen Verlustlosigkeit der Bauelemente. Mit der gerade eingeführten Normierung (f / f_g)² = v² erhalten wir:

(18a)          U₂ / U₁ = - v² / (1- v²)

2.2 Einfache Filter zwischen Endverstärkern und Lautsprechern

Verwendet man die oben angegebenen Hoch- und Tiefpässe als Filter (Weichen) vor Lautsprechern, dann muss man von der idealisierenden Annahme i₂ = 0 absehen. Denn der komplexe oder angenähert reelle Widerstand eines Lautsprechers ist nicht hochohmig gegenüber dem ausgangsseitigen Widerstand eines Filters. Wir werden daher den Lautsprecherwiderstand nachfolgend durch R_L (in der Zeichnung RL) berücksichtigen. Wir schließen R_L zuerst an den Ausgang eines Tiefpasses, bestehend aus L und C, an.

Schaltbild: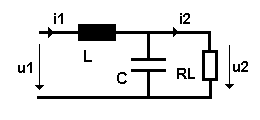

Rechnerisch müssen wir die Parallelschaltung von R_L mit C berücksichtigen. Wir beginnen mit den allgemeinen komplexen Widerständen Z₁ im Längszweig und Z₂^* im Querzweig der vorangehenden Schaltung. Dabei beinhaltet Z₂^* die Parallelschaltung aus Z₂ mit R_L.

(19)            û₂ / û₁ = Z₂^* / (Z₂^* + Z₁) = Zähler / Nenner

Der Bruch wird unübersichtlich, wenn wir ihn nicht aufteilen:

      Zähler von (19):       Z₂^* = Z₂ R_L / (Z₂ + R_L) und der

      Nenner von (19):       Z₂^* + Z₁ = Z₂ R_L / (Z₂ + R_L) + Z₁)      zusammengefasst erhalten wir:

(19a)               û₂ / û₁ = Z₂ R_L / (Z₂ R_L +Z₁ R_L + Z₁ Z₂ )

Nach kurzer Umformung erhalten wir:

(20)            û₂ / û₁ = R_L / (R_L - ω²LC R_L + jωL)

Will man den zu Gl.(20) gehörenden Graph aufzeichnen, so braucht man dazu wieder den Betrag. Er ist, wie oben beschrieben wurde, die Quadratwurzel aus Realteil im Quadrat plus Imaginärteil im Quadrat. Das betrifft hier den Nenner von Gl.(20):

(21)            U₂ / U₁ = R_L / [ (R_L - ω²LCR_L)²+(ωL)²]^1/2. = [ (1-ω²LC)² + (ωL / R_L)² ] ^-1/2

Beim Hochpass geht man entsprechend vor und setzt unter Berücksichtigung des Lautsprecherwiderstandes R_L an Stelle von Z₁ den Blindwiderstand 1/jωC des Kondensators und an Stelle von Z₂ den Blindwiderstand jωL der Spule ein, so dass nach kurzer Umformung der folgende komplexe Spannungsteiler entsteht:

(22)            û₂ / û₁ = -ω²LCR_L / (R_L - ω²LCR_L + jωL)

Der Betrag davon lautet:

(23)            U₂ / U₁ = ω²LC / [ (1 - ω²LC)² +(ωL / R_L)²]^1/2

Schaltbild: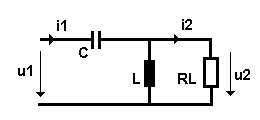

Das waren nur einfachste Tief- und Hochpässe als Fillter (Weichen) vor Lautsprechern. Tatsächlich verwendet man viel kompliziertere Schaltungen, auch Bandpässe, die nach oben und nach unten hin nur einen bestimmten Frequenzbereich passieren lassen, die aber alle auf den gezeigten Grundstufen aufbauen. Die tatsächliche Dimensionierung beruht dann auf einem gemischten Verfahren unter Anwendung spezieller Dimensionierungsverfahren und akustischen Messungen.
 
zurück zur Übersicht