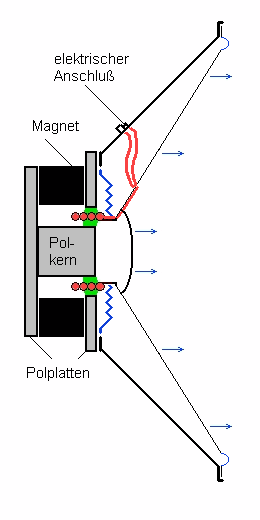
Links ist der Aufbau des Lautsprechers skizziert. Grob gesagt
besteht er aus einer Membran und einem Antriebsystem. Das Antriebssystem
besteht aus einem Magneten, der die Aufgabe hat, im grün eingezeichneten
Bereich ein Feld zu erzeugen.
In diesem Bereich liegt die stromdurchflossene Schwingspule (rot).
In ihr wird eine Kraft F erzeugt, die senkrecht zum Magnetfeld und
senkrecht zum Stromfluss des Leiter wirkt. Im Bild, wo
- das Magnetfeld von unten nach oben bzw. umgekehrt läuft
- der Strom senkrecht zur Bildebene fließt, ist die
- resultierende Kraft senkrecht zu beiden: horizontal gerichtet.
Welche Größen sind für den Antrieb bestimmend?
a) die Stärke des Magnetfelds und seine Ausdehnung
b) die Schwingspule mit ihren Eigenschaften
Der Strom, der durch die Spule fließt, erzeugt dort, wo sie im
Magnetfeld ist, eine Kraft F:
|
F = (sm * B) * I, (Gleichung 1)
|
wobei sm die Länge des Drahtes im Magnetfeld (oder
die Anzahl der Windungen im Magnetfeld mal Umfang einer Windung),
B die Stärke des Magnetfelds und I die Stromstärke ist.
Dabei nennt man den Ausdruck in der Klammer auch den Kraftfaktor F/I oder B*L
(hier steht L für Länge, wir wollen aber s für
Länge benutzen, da wir L für Induktivität benötigen)
Legt man also an den Lautsprecher einen Strom I an, so wird abhängig vom
Kraftfaktor die Membran mit einer bestimmten Kraft F ausgelenkt F = (sm * B) * I.
Wie groß ist aber der Strom, der durch die Lautsprecherspule fließt? Hierzu sind
noch weitere Größen einzuführen.
1. Das ohmsche Gesetz:
Es besagt, dass mit dem Strom I
|
UR = R * I, (Gleichung 2)
|
wobei UR die Spannung am Lautsprecher und R der ohmsche Widerstand ist.
Wenn man keinen Wechselstrom, sondern Gleichstrom anlegt, ist dies richtig.
Wir legen im folgenden Wechselstrom an, und meinen mit den Größen I, U komplexe Amplituden.
2. Die induzierte Spannung
Bewegt sich die Schwingspule im Magnetfeld, so wird in der Schwingspule
eine Spannung Ui induziert:
|
Ui = (sm * B) * v, (Gleichung 3)
|
wobei sM die Länge des Drahtes im Magnetfeld, B die Flussdichte des Magneten und
v die Geschwindigkeit der Schwingspule ist.
Demnach ist die induzierte Spannung vom Kraftfaktor und der Geschwindigkeit der Spule
abhängig.
3. Spannung an einer Induktivität
Durch den wechselnden Strom gibt es in der Spule, die eine Induktivität hat,
ebenso eine Spannung: UL
|
UL = j ω L * I, (Gleichung 4)
|
wobei j beschreibt, dass UL gegenüber I um 90 Grad voraus eilt und ω die Kreisfrequenz ist,
also 2 * π * Frequenz f.
Gleichungen für den Antrieb
Somit gilt für den Antrieb, wobei die Spannung am Lautsprecher Ug
sich aus den Einzelspannungen zusammen setzt: Uges = UR + Ui + UL,
also die Werte jeweils eingesetzt:
Uges = R * I + (sm * B) * v + j * ω * L * I, (Gleichung 5)
|
Hierbei sind die Summanden wieder komplexe Amplituden, d.h. man darf sie nicht skalar addieren.
Legt man eine Spannung an den Lautsprecher an, so teilt sich diese Spannung für
3 unterschiedliche "Aktivitäten" auf (siehe auch Bild rechts):
a) UR = R * I wird als Wärme in der Schwingspule umgesetzt
b) UL = j * ω * L * I dient dem Umladen der Spule
c) Ui = sm * B * v entspricht der Bewegung der Membran
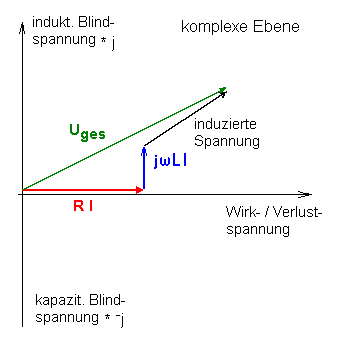
Je weniger Leistung in a) umgesetzt wird, desto höher kann der Wirkungsgrad des
Lautsprechers sein. b) schaukelt die Leistung in den Lautsprecher und heraus
(dies ist die Eigenschaft einer Spule) und c) ist für den Antrieb zuständig;
diese Energie wird in mechanische Energie umgewandelt.
Mit einer Spule, die unendlich niederohmig ist (Supraleiter) und die kaum
Induktivität hat, wäre alleine Anteil c) wirksam. Dann würde gelten:
sm * B * v = Ui (Gleichung 6),
|
wodurch die Phase von Membranbewegung und Spannung genau 90 Grad verschoben wäre,
denn die Geschwindigkeit ist im Nulldurchgang der Membran an höchsten, wenn
die Spannung gerade ihren Maximalwert erreicht.
Da die Hantierung mit dem Gleichungssystem schwierig ist und der Übergang des
Schalls von der Membran zur Luft ebenso eingeht, haben Thiele und Small
ihr Modell entwickelt mit dem man die Tieftoneigenschaften mit den Parametern:
- Gesamtgüte Qts
- Resonanzfrequenz f0 (oder fe genannt)
- Äquivalenzvolumen VAS
bestimmen kann. Dazu stellen wir Ihnen kostenfrei verschiedene Programme in der
Rubrik Tools zur Verfügung.
|